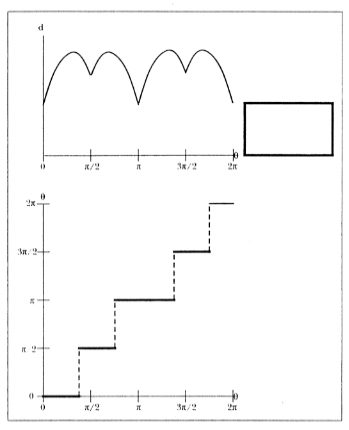
Figure 5: The diameter function (top) and squeeze function (bottom) for the rectangular part.
We assume that:
These assumptions are similar to those made by Brost [2], and Taylor, Mason and Goldberg [21]. Assumptions 2, 6, and 8 simplify the analysis and improve the combinatorics of the search. By restricting gripper motion to be orthogonal to the jaws (Assumption 2), we obtain a one-dimensional action space. The frictionless gripper (Assumption8) insures that the state space is the finite set of stable part orientations. Assumtion 6 simplifies the mechanical analysis. In a later section (Discussion), we discuss how this assumption can be relaxed by considering the related class of push-grasp actions.

Figure 5: The diameter function (top) and squeeze function (bottom) for the rectangular part.
When a part is grasped with the frictionless gripper, it assumes one of a
finite number of stable orientations corresponding to local minima in a
diameter function. Let a two-dimensional part be described with a
continuous curve, , in the plane. The distance between two
parallel tangent lines varies with the orientation of the lines. Let
be the set of planar orientations. The diameter function,
, is the distance between parallel tangents at angle
.
For polygonal parts, the diameter function is piecewise sinusoidal
(Figure 5; top).
When a part is grasped between the jaws, the distance between the jaws corresponds to the diameter. Closing the jaws changes the diameter and thus the relative orientation of the part. The jaws continue closing until the diameter is at a local minimum that also defines a stable orientation of the part. The diameter function can be viewed as a potential energy function for a conservative system [6].
During a squeeze action, part motion is determined by the diameter
function. That is, given an initial orientation of the part with respect
to the gripper, the part's final orientation can be determined from the
diameter function. A transfer function, relating initial orientations to
final orientations, can be represented with a piecewise constant squeeze function , .
We define the squeeze function such that if is the initial orientation
of the part with respect to the gripper,
is the final orientation
of the part with respect to the gripper. The squeeze function can be
derived from the diameter function as follows. All orientations that lie
between a pair of adjacent local maxima in the diameter function will map
into the same final orientation. The squeeze function is constant over
this interval of orientations. Each local maximum in the diameter function
corresponds to a discontinuity in the squeeze function. In order for the
squeeze function to be single-valued, we assume that all steps are closed
on the left (Figure 5; bottom).
Note that the squeeze function has period due to rotational symmetry
in the gripper. Rotational symmetry in the part also introduces
periodicity into the squeeze function. In general the squeeze function has
period
such that
Periodicity in the squeeze function gives rise to aliasing, where the
part in orientation behaves identically to the part in
. Any
sequence of actions that maps
to
will map
to
.
This implies that no sequence of squeeze-grasp actions can map orientations
and
into a single final orientation. Thus a part can only be
oriented up to symmetry in its squeeze function.
For a given part, letFor example, for a part with no rotational symmetry, a squeeze plan orients the part up to symmetry if the plan that yields exactly two final statesbe the smallest period in its transfer function. We say that a plan orients a part up to symmetry if the set of possible final states includes exactly
states that are equally spaced on
.
The algorithm requires that the transfer function is a monotonically nondecreasing step function on the space of planar orientations. The squeeze function satisfies these conditions as does the push-grasp function defined in the Discussion section.